heihei12305

1.格路问题


！！复习算法考试所用，代码为老师课堂手写，逻辑没错，应该有点小问题，而且一看就莫得main函数，需要修改才能运行，仅供思路参考


欲求从左下角到右上角的最短路径



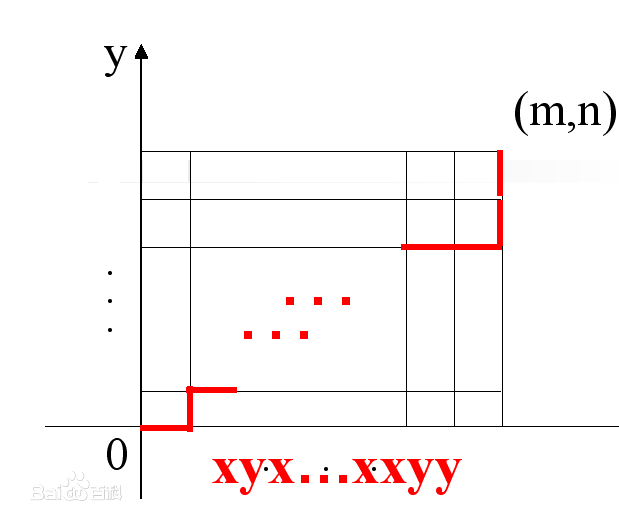
通过方法


使得r向右，u向上


1.r,r,r.....(m个)，u,u,u,u,u,u(n个)


2.u,u,u,u,u,u(n个)，r,r,r.....(m个)


一条路径为由m个r，n个u 构成的排列！共（m+n）!/(m!*n!)


蛮力做法构造（m+n）!/(m!+n!)个路径，需加法（m+n）!/(m!*n!)*（m+n-1）次,比较（m+n）!/(m!*n!)-1次


注：（m+n）!/(m!*n!) 为指数级别


下面为实现代码

	template<class T>
	struct TPoint{
		T r,u;//向右，向上的距离
		T d;//从0到此点的最短路径长
		int from; // 0:无最短路径  1：左  2：右
		TPoint():from(0),d(-1){}
	}；
	ps: struct与class区别？  只有一点  声明默认等级不同  struct->public，class->private
	分析：p.d= {
		0 p为起点
		L(p).d+L(p).r  p为最底排
		D(p).d+D(p).u   p为最左排的列
		min(L(p).d+L(p).r,D(p).d+D(p).u)   其他
	初始化： int m=...,n=...;
	TPoint<float> **g = new TPoint<float> *[m+1];  实例化 行
	for(int i = 0;i<=m;i++)   实例化 每个行上的列
	{
			g[i] = new TPoint<float>[n+1];
	}
	//至此  实例化出g[i][j] ;  0<=i<=m;  0<=j<=n;
	
	//初始化二维表格
	for(int i = 0;i<=m;i++)
	{
		for(int j = 0;j<=n;j++)
		{
			g[i][j].r = rand(); 
			g[i][j].u = rand(); 
		}
	}
	//DP方法（动态规划方法）
	//1.先计算最简单的子问题
	//最下一排
	for(int i = 1;i<=m;i++)
	{
		g[i][0].d = g[i-1][0].d + g[i-1][0].r;
		g[i][0].from  = 1;//left
	}
	//最左一排
	for(int j = 1;j<=n;j++)
	{
		g[0][j].d = g[0][j-1].d + g[0][j-1].u;
		g[0][j].from = 2;//down
	}
	//自顶向上依次求解问题
	for(int j = 1;j<=n;j++)
	{
		for(int i = 1;i<=m;i++)
		{
			//以下计算g[i][j]
			//定义三个引用p,l,d
			TPoint<float> &p = g[i][j];
			TPoint<float> &L = g[i-1][j];
			TPoint<float> &D = g[i][j-1];
			float dL = L.d + L.r;
			float dD = D.d + D.u;
			if(dL<dD)
			{
				p.d = dL;
				p.from = 1;//left
			}
			else{
				p.d = dD;
				p.from = 2;//down
			}
		}
	}
	//构造解
	//方法一，采用动态数组  stl 中的 vector
	std::vector<char> v;
	int i = m , j = n;
	while(i>0||j>0)
	{
		TPoint<float> &P = g[i][j];
		if(p.from == 1) //左侧
		{
			v.push_back('r');
			i--;
		}
		else
		{
			v.push_back('n');
			j--;
		}
	}
	//打印解 //v[k-1],v[k-2].......v[0]
	int k = v.size();
	for(int i = k-1;i>=0;i--)
	{
		cout<<v[i];
	}
	//方法二 采用栈 stack
	std::stack<char> s;
	int i = m , j = n;
	while(i>=0||j>=0)
	{
		if(g[i][j].from==1)//left
		{
			s.push('r');
			i--;
		}
		else{
			s.push('u');
			j--;
		}
	}
	//打印，依次出栈
	while(!s.emptu())
	{
		cout<<s.top();
		s.pop();
	}
	
	//!!!!来到了重点    c++没有自动的内存回收机制，要手动释放
	//清理工作，释放内存
	for(int i = 0;i<=m;i++)
	{
		delete[] g[i];
	}
	delete[] g;