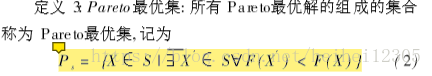MOPSO

https://heihei12305.github.io/MOPSO/

1.0 版本 pso 部分

&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp最近做大创开始学习遗传算法，粒子群算法等,在大佬的带领下，开始写点博客，因为是第一次写，而且自己学的也不好(捏个是重点)，就当写给自己看啦。
&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp粒子群算法跟遗传算法一样，都是从自然界的自然现象得到启发，而被大牛创造出来的，在一代代的改进中逐渐趋于完善，也慢慢作用于越来越多的领域中。
&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp粒子群算法据说是从鸟群寻食中得到的启发，一群鸟在一个不知道食物分布的地方觅食，它们会渐渐集中到食物最多的地方去，当然，如果地方太大的话，也可能会出现多个集中鸟比较多的地方。<font color=#0099ff size=5 face="STCAIYUN">这里头有几个官方术语</font>

</img>

&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp个人理解就是一个较优解集支配一个次优解集

</img>

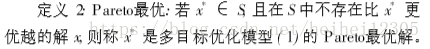
&nbsp&nbsp&nbsp&nbsp&nbsp&nbspPareto最优就是在最理想条件下，我们取得了自己最想要的结果，但是很遗憾，因为现实问题的影响因素太多，所以我们往往陷入局部最优，或者得到一堆较优解。于是：

在这里插入图片描述

&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp根据我们计算得到的最优解集，我们可以计算出理想的最终优化结果，就像如果发电的模型的话，我们可以得到我们想要的发电的效率啦，参量啦~~~也就是

</img>

&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp下面的是一个在matlab上已经测试通过的 z = x^2 + y^2的pso实现全部代码，希望对大家有帮助。
下文代码参考该博主代码写出，这个博客讲PSO很赞哎！

https://blog.csdn.net/zyqblog/article/details/80829043

close all;
clc;
N = 100;%种群规模
D = 2;%粒子维度
T = 100;%迭代次数
Xmax = 2000;
Xmin = -2000;
c1 = 1.5; %学习因子1
c2 = 1.5; %学习因子2
w = 0.8; %惯性权重
Vmax = 10; % 最大飞行速度
Vmin = -10;% 最小飞行速度
popx = rand(N,D)*(Xmax-Xmin)+Xmin;% 初试化粒子群的位置(粒子位置是个D维向量)
popv = rand(N,D)*(Vmax-Vmin)+Vmin;%初始化粒子群的速度（粒子速度是个D维向量）
%初始化每个历史最优粒子
pBest = popx;
pBestValue = func_fitness(pBest);
%初始化全局历史最优粒子
[gBestValue,index] = max(func_fitness(popx));
gBest = popx(index,:);
for t=1:T
    for i=1:N
        %更新个体的位置和速度
        popv(i,:) = w*popv(i,:)+C1*rand*(pBest(i,:)-popx(i,:))+C2*rand*(gBest-popx(i,:));
        popx(i,:) = popx(i,:)+popv(i,:);
        %边界处理，超过定义域范围就取该范围极值
        index = popv(i,:)>Vmax | popv(i,:)<Vmin ;
        popv(i,index) = rand*(Vmax-Vmin)+Vmin ;
        index = find(popx(i,:)>Xmax | popx(i,:)<Xmin);
        popx(i,index) = rand*(Xmax-Xmin) + Xmin;
        %更新粒子历史最优
        if func_fitness(popx(i,:))>pBestValue(i)
            pBest(i,:) = popx(i,:);
            pBestValue(i) = func_fitness(popx(i,:));
        elseif pBestValue(i)>gBestValue
            gBest = pBest(i,:);
            gBestValue = pBestValue(i);
        end
    end
      %每代最优解对应的目标函数值
      tBest(t) = func_objValue(gBest);%目标函数
end
figure
plot(tBest);
xlabel('迭代次数');
ylabel('适应度值');
title('适应度·进化曲线');

function [result] = func_fitness(pop)
%UNTITLED2 此处显示有关此函数的摘要
%   此处显示详细说明
objValue = func_objValue(pop);
result = 1314 -objValue ;
end

function [result] = func_objValue(pop)
%NTITLED3 此处显示有关此函数的摘要
%   此处显示详细说明
objValue = sum(pop,2);
result = objValue;
end

2.0版，MOPSO部分，文件在这 main.m

@TOC

决定走前端这条路了，不过MOPSO我还是有研究了很久的，大概因为是本科实力不够吧，创新无力，所以只能做到复现，就到这吧，留下这篇文章，后来者少踩点坑吧。

看到MOPSO了，想必已经了解了PSO了，不需要要再赘述这些是什么了。

介绍下下面的MOPSO文件吧

里面有一个电厂约束函数的参数 Varin = load('mydata.mat');%导入了约束函数的参数，以及一个电厂的约束函数，不过一般用ZDT 1,2,3就够了。 ``` function fv = fitness2(x,~,Varin) res1=0; res2=0; for i=1:6 res1 = res1+Varin.a(i)x(i)x(i)+Varin.b(i)x(i)+Varin.c(i); res2 = res2+Varin.Ea(i)x(i)x(i)+Varin.Eb(i)x(i)+Varin.Ec(i)+Varin.Ed(i)exp(Varin.Ee(i)x(i)); end fv(1) = res1; fv(2) = res2;

end

2. 参看论文有改过几个地方，不过个人感觉不重要。关键点在p189行那, 毫无疑问，这是一种取巧做法，是不可取的，但实在是创新无力，参考ZDT函数特性改的，做法很不可取，读者要是用这个代码，心里有点数哈~~~

if x(i,j)<Varin.pMin(j) if(randi([0,0],1)==0) x(i,j)=Varin.pMin(j);
v(i,j)=-v(i,j)unifit; if(unifit>0.2) unifit = unifit -0.1; end else x(i,j)=Varin.pMin(j)+(Varin.pMax(j)-Varin.pMin(j))rand; %随机初始化位置
v(i,j)=(Varin.pMax(j)-Varin.pMin(j))rand0.5; end end

3. 这个代码跑的奇慢无比其他的倒都是正常的MOPSO代码了，嘿嘿，我就到这了，要加油丫。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % 改进的多目标粒子群算法，包括多个测试函数 % 对程序中的部分参数进行修改将更好地求解某些函数 %% 主函数 function []=main() Varin = load(‘mydata.mat’);%导入了约束函数的参数 ZDTFV=cell(1,50); %// 创建元胞数组 ZDT=zeros(1,50); %//0矩阵 funcname = ‘ZDT1’; times = 10;%相当于独立运行十次程序 M = 100;%MOPSO中的迭代次数 for i=1:times %//循环10次，做以下的迭代 tic; %//计时开始 %[np,nprule,dnp,fv,goals,pbest]=ParticleSwarmOpt(funcname,100,200,2.0,1.0,0.5,M,30,Varin);%–ZDT3 zeros(1,9)-5-》zeros(1,29) [np,nprule,dnp,fv,goals,pbest]=ParticleSwarmOpt(funcname,100,200,2.0,1.0,0.4,M,10,[0,zeros(1,9)],[1,zeros(1,9)+5],Varin);%–ZDT4 elapsedTime=toc; %//计时结束 ZDTFV(i)={fv}; ZDT(i)=elapsedTime; display(strcat(‘迭代次数为’,num2str(i))); end zdt1fv=cell2mat(ZDTFV’); for i =1:times display(strcat(i,’:’)); disp(ZDT(i));%也就是用时啦 end disp(zdt1fv); disp(‘接下来，更新后的适应度值为：’); zdt1fv=GetLeastFunctionValue(zdt1fv); disp(zdt1fv); figure(9) plot(zdt1fv(:,1),zdt1fv(:,2),’k*’); %以下设置坐标轴的字体形式和大小 xlabel(‘$f_1$’,’interpreter’,’latex’,’FontSize’,25); ylabel(‘$f_2$’,’interpreter’,’latex’,’FontSize’,25); set(gca,’FontName’,’Times New Roman’,’FontSize’,25)%设置坐标轴字体和刻度的大小,get current axes返回当前坐标轴对象的句柄值 %if(strcmp(funcname,’ZDT3’)) axis([0 1 0 1]); %else % axis([20555 20790 190.4 190.7]); %end

% 以下求收敛度 % 先均匀取真实Pareto最优解上的点，再求其两目标函数值 p_true=0:0.002:1; pf_true1=p_true; pf_true2=1-p_true.^2; r=size(zdt1fv,1);

for i=1:r%对每一个非劣解， for j=1:501 d(i,j)=sqrt((zdt1fv(i,1)-pf_true1(j))^2+(zdt1fv(i,2)-pf_true2(j))^2); end end %下面对d中每行求最小值，即为第i个点与各点的最小距离 for i=1:r dmin(i)=min(d(i,:)); end Cmean=mean(dmin); %Cfangcha=var(dmin)% 各数与均值的差的平方，除以个数-1，这是样本方差 disp(‘样本均值:’); disp(Cmean); Cvariance=var(dmin,1);% 各数与均值的差的平方，除以个数,这是数学上方差的定义 disp(‘样本方差:’); disp(Cvariance) % 下面求多样性delta % 先对zdt1fv按第一列升序排序，即按横坐标（第一个目标值）从左到右 zdt1fv=sortrows(zdt1fv);%按第一列升序排序结束，下面计算df(与左边的极值解前沿的距离)和dl（与最右边的极值解前沿的距离） df=sqrt((zdt1fv(1,1)-0)^2+(zdt1fv(1,2)-1)^2); r=length(zdt1fv); dl=sqrt((zdt1fv(r,1)-1)^2+(zdt1fv(r,2)-0)^2); for i=1:r-1 %第i个和第i+1个解前沿之间的距离为d(i) c(i)=sqrt((zdt1fv(i,1)-zdt1fv(i+1,1))^2+(zdt1fv(i,2)-zdt1fv(i+1,2))^2); end %下面求d的均值 meanNum=mean(c); %代入公式计算delta的值 %先求和号的部分 sum=0; for i=1:r-1 sum=sum+abs(c(i)-meanNum); end delta=(df+dl+sum)/(df+dl+(r-1)*meanNum); disp(‘多样性为：’); disp(delta);

end %% MOPSO函数定义 %function [np,nprule,dnp,fv,goals,pbest] = ParticleSwarmOpt(funcname,N,Nnp,cmax,cmin,w,M,D,Varin) function [np,nprule,dnp,fv,goals,pbest] = ParticleSwarmOpt(funcname,N,Nnp,cmax,cmin,w,M,D,lb,ub,Varin) %待优化的目标函数:fitness %电厂约束函数：fitness2 %内部种群(粒子数目)：N %外部种群(非劣解集):Nnp %适应度参数 %学习因子1:cmax %学习因子2:cmin %惯性权重:w %最大迭代次数：M %问题的维数：D %目标函数取最小值时的自变量值:xm %目标函数的最小值:fv %迭代次数:cv %非劣检查:flag %自适应度参数:unifit:1->0.1

format long; unifit = 1; flag = 0; NP=[];%非劣解集 Dnp=[];%非劣解集距离 params = struct(‘isfmopso’,true,’istargetdis’,false,’stopatborder’,true);%ZTD2->isfmopso(false->true)改了一下 ZTD3问题时应为true %x0=lb+(ub-lb).*rand([1,D]); %T=size(fitness(x0,funcname),2); T = 2; goals=zeros(M,N,T);%记下N个粒子M次迭代T维目标变化

% %—-初始化种群的个体——–///////第1步/////////////////////////////////// % %x(1,:)=x0; % %v(1,:)=(ub-lb).rand([1,D])0.5; x = zeros(N,D); v = zeros(N,D); % for i=1:N % for j=1:D % x(i,j)=lb(j)+(ub(j)-lb(j))rand; %随机初始化位置 % v(i,j)=(ub(j)-lb(j))rand0.5; %随机初始化速度 % end % end % %—-计算目标向量———- % %—速度控制 % %vmax=(ub-lb)0.5; %vmin = -vmax;

%—-初始化种群的个体——–///////第1步///////////////////////////////////

for i=1:N for j=1:D x(i,j)=lb(j)+(ub(j)-lb(j))rand; %随机初始化位置 v(i,j)=(ub(j)-lb(j))rand0.5; %随机初始化速度 end end %—-计算目标向量———- %—速度控制 vmax=(ub-lb)0.5; vmin= -vmax;

%—–求出初始NP———–////////第2步/////////////////////////////////// NP(1,:)=x(1,:);%第一个默认加入（非劣解集），粒子为一行不确定列的，列数表示决策变量数，即问题的维数 NPRule=[0,0,0];%非劣解集参数 Dnp(1,1)=0;

for i=2:N

  [NP,NPRule,Dnp,flag] = compare(flag,x(i,:),NP,NPRule,Dnp,Nnp,funcname,params,Varin); end %-----初始自身最好位置------///////第3步//////////////////////////////////// pbest = x;%自身最优解

%—–在确定每个粒子所对就的目标方格——-//第4步///////////////////////////

%——进入主要循环，按照公式依次迭代———— for t=1:M
c = cmax - (cmax - cmin)t/M; w1=w-(w-0.3)t/M;

for i=1:N %-----获得全局最优-------/////第5步/////////////////////////////////////////////   
  [gbest,NPRule] = GetGlobalBest(NP,NPRule,Dnp);    
      v(i,:)=w1*v(i,:)+c*rand*(pbest(i,:)-x(i,:))+c*rand*(gbest-x(i,:));
      for j=1:D
        if v(i,j)>vmax(j) 
            v(i,j)=vmax(j);
        elseif  v(i,j)<vmin(j) 
            v(i,j)=vmin(j);
        end 
      end
       x(i,:)=x(i,:)+v(i,:); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %-------------------采取措施，避免粒子飞出空间----------////第7步/////////////
     %速度位置钳制
    if(params.stopatborder)%粒子随机停留在边界    
        if x(i,1)>ub(1)
            x(i,1)=ub(1);
            v(i,1)=-v(i,1);
        end
        if x(i,1)<lb(1)
             x(i,1)=lb(1)+(ub(1)-lb(1))*rand;  %随机初始化位置        
             v(i,1)=(ub(1)-lb(1))*rand*0.5; 
        end
        for j=2:D
            if x(i,j)>ub(j)
                if(randi([0,2],1)==0)%改了0->1
                    x(i,j)=ub(j);
                    v(i,j)=-v(i,j);
                else
                     x(i,j)=lb(j)+(ub(j)-lb(j))*rand;  %随机初始化位置
                     v(i,j)=(ub(j)-lb(j))*rand*1.5; 
                end              
            end
            if x(i,j)<lb(j)
                if(randi([0,0],1)==0) 
                  x(i,j)=lb(j);              
                  v(i,j)=-v(i,j)*unifit;
                   if(unifit>0.2)
                       unifit = unifit -0.1;
                   end
                else
                   x(i,j)=lb(j)+(ub(j)-lb(j))*rand;  %随机初始化位置        
                   v(i,j)=(ub(j)-lb(j))*rand*0.5; 
                end
            end
        end
    end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%         %------------------每个粒子的目标向量-----------------//第8步///////////////  
    goals(t,i,:)=fitness(x(i,:),funcname,Varin); %----------------调整自身---------------------------//第9步/////////////////
    domiRel = DominateRel(pbest(i,:),x(i,:),funcname,params,Varin);%x,y的支配关系
   if domiRel==1%pbest支配新解
       continue;
   else 
        if domiRel==-1%新解支配pbest
            pbest(i,:) = x(i,:);
          elseif(rand*2<1)%新解与pbest互相不支配
            pbest(i,:) = x(i,:);
        end %-----------------对NP进行更新和维护-----------------//第10步////////////////
      
      [NP,NPRule,Dnp,flag] = compare(flag,x(i,:),NP,NPRule,Dnp,Nnp,funcname,params,Varin);
      if flag==1%为克服本算法易陷入局部最优的问题，引入非劣排查监测机制
         [NP,flag,x,v] = fresh(NP,flag,x,v);
      end
   end
end end np = NP;%非劣解 nprule=NPRule; dnp = Dnp;%非劣解之间的距离 r=size(np,1); fv=zeros(r,T); for i=1:r
fv(i,:)=fitness(np(i,:),funcname,Varin); end end %%%%%%%%%%%%%%%--------------主函数结束--------------%%%%%%%%%%%%%%%%% %% 将粒子维护到外部种群 function [np_out,nprule_out,dnp_out,flag] = compare(flag,x,np,nprule,dnp,nnp,funcname,params,Varin) %np:现有非劣解 %x:需要比较的量 Nnp = nnp;%非劣解集空间 r=size(np,1);%非劣解的个数 np_out=np;%非劣解复本 nprule_out = nprule; dnp_out = dnp;%非劣解集点之间距离 if r==0
return; end for i=r:-1:1
domiRel=DominateRel(x,np(i,:),funcname,params,Varin);
if domiRel==1 %NP(i)被x支配
    np_out(i,:)=[];%非劣解剔除该解
    nprule_out(i,:)=[];
    dnp_out(i,:)=[];  
    if ~isempty(dnp_out)
        dnp_out(:,i)=[];
    end
elseif domiRel==-1 %x被NP(i)支配,返回不再比较
    return;
end end r1=size(np_out,1);%现有非劣解的行列 np_out(r1+1,:)=x;%与所有非支配集粒子比较均占优或不可比较，则NP中加入x

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

nprule_out(r1+1,:)=[0,0,0];

if r1==0 dnp_out=0; end for j=1:r1 dnp_out(r1+1,j)=GetDistance(np_out(j,:),x,funcname,params); dnp_out(j,r1+1)=dnp_out(r1+1,j); end if r1>=Nnp %达到非劣解种群极限 %———移除密集距离最小的一个——- densedis = GetDenseDis(dnp_out);
n_min = find(min(densedis)==densedis);%找出密度距离最小的一个 tempIndex = randi([1,length(n_min)],1);
if min(densedis)==0 flag = 1; end np_out(n_min(tempIndex),:)=[];%非劣解剔除该解 nprule_out(n_min(tempIndex),:)=[]; dnp_out(n_min(tempIndex),:)=[]; if ~isempty(dnp_out) dnp_out(:,n_min(tempIndex))=[]; end end end %% 求两向量之间的距离 function dis=GetDistance(x,y,funcname,params) if(params.istargetdis) gx=fitness(x,funcname,Varin); gy=fitness(y,funcname,Varin); gxy=(gx-gy).^2; dis=sqrt(sum(gxy(:))); else g=x-y; dis=sum(sum(g.^2)); end end %% 密集距离（最近的距离） function densedis = GetDenseDis(dnp) [r,c] = size(dnp); densedis=zeros(1,r); for i=1:r firstmin=Inf; for j=1:c if dnp(i,j)~=0 && dnp(i,j)<firstmin firstmin = dnp(i,j); end
end densedis(i)=firstmin; end end %% 稀疏距离（第二近的距离） function sparedis = GetSpareDis(dnp) [r,c] = size(dnp); sparedis=zeros(1,r); for i=1:r firstmin=Inf; secondmin=Inf; for j=1:c if dnp(i,j)~=0 && dnp(i,j)<firstmin firstmin = dnp(i,j); end if dnp(i,j)~=0 && dnp(i,j)~=firstmin && dnp(i,j)<secondmin secondmin = dnp(i,j); end
end sparedis(i)=(firstmin+secondmin)/2; end end %% 比较两粒子的相互支配关系 function v = DominateRel(x,y,funcname,~,Varin) %判断x与y支配关系,返回1表示x支配y，返回-1表示y支配x,返回0表示互不支配 v=0; gx = fitness(x,funcname,Varin);%x的目标向量 gy = fitness(y,funcname,Varin);%y的目标向量 len = length(gx); if sum(gx<=gy)==len%x的所有目标都比y小，x支配y v=1; elseif sum(gx>=gy)==len%y的所有目标都比x小，y支配x v=-1; end end %% 随机取一个全局最优 function [gbest,nprule_out] = GetGlobalBest(np,nprule,dnp_out) r=size(np,1);%非劣解的行列 nprule_out=nprule; intem=1; if(round(rand)==0) if r==1
gbest = np(1,:); else sparedis = GetSpareDis(dnp_out); if(round(rand)==0) n_max=find(max(sparedis)==sparedis); intem=n_max(round(rand(length(n_max)-1)+1)); gbest = np(intem,:);
else %添加了寻找最小的操作 sparedis = GetSpareDis(dnp_out); n_min=find(min(sparedis)==sparedis); intem=n_min(round(rand(length(n_min)-1)+1)); gbest = np(intem,:); end

end     else 
tt=find(min(nprule(:,1))==nprule(:,1));  %随机取一个作为全局最优，看曾经被选过的次数最低的优先选
intem=tt(round(rand*(length(tt)-1)+1));
gbest = np(intem,:);       end nprule_out(intem,1)=nprule_out(intem,1)+1;%对于选取的粒子，将nprule（行数同np，列数为3）中对应此 %行的第一列的数值加1，因为此列记录粒子被选取过的次数，将来作为是否再次将其选为全局极值的参考。 end %% 电厂约束函数 function fv = fitness2(x,~,Varin)
res1=0;
res2=0;
for i=1:6
    res1 = res1+Varin.a(i)*x(i)*x(i)+Varin.b(i)*x(i)+Varin.c(i);
    res2 = res2+Varin.Ea(i)*x(i)*x(i)+Varin.Eb(i)*x(i)+Varin.Ec(i)+Varin.Ed(i)*exp(Varin.Ee(i)*x(i));
end
fv(1) = res1;
fv(2) = res2;

end %% ZDT1,ZDT2,ZDT3测试函数 function fv=fitness(x,funcname,~) %获得多目标的目标向量 fv fv=[]; switch upper(funcname) case ‘ZDT1’ n=length(x); gv=1+9sum(x(2:n))/(n-1); fv(1)=x(1); fv(2)=gv(1-sqrt(x(1)/gv)); case ‘ZDT2’ n=length(x); gv=1+9sum(x(2:n))/(n-1); fv(1)=x(1); fv(2)=gv(1-(x(1)/gv).^2); case ‘ZDT3’ n=length(x); gv=1+9sum(x(2:n))/(n-1); fv(1)=x(1); fv(2)=gv(1-sqrt(x(1)/gv)-(x(1)/gv)sin(10pix(1)));
case ‘ZDT4’ n=length(x); gv=1+10(n-1)+sum(x(2:n).^2-10cos(4pix(2:n))); fv(1)=x(1); fv(2)=gv(1-sqrt(x(1)./gv)); end end %% 剔除外部种群中的非支配集 function fvout=GetLeastFunctionValue(fvin) fvout=fvin; n=size(fvout,1); i=1; while(i<=n) j=i+1; isdominated=false;%判断条件 while(j<=n) a=fvout(i,:);b=fvout(j,:); if((a(1)<b(1)&&a(2)<=b(2))||(a(1)<=b(1)&&a(2)<b(2)))%b被a支配了 fvout(j,:)=[];n=n-1; else if((b(1)<a(1)&&b(2)<=a(2))||(b(1)<=a(1)&&b(2)<a(2)))%a被b支配了 isdominated=true; end j=j+1; end end if isdominated fvout(i,:)=[];n=n-1; else i=i+1; end end end %% flag为1,说明结果可能陷入局部最优，故加入25%新鲜粒子 function [NP,flag,x,v] = fresh(NP,~,x,v) r=size(NP,1); flag =1; for i=2:r if(randi([0,3],1)==0) for j=1:D x(i,j)=lb(j)+(ub(j)-lb(j))rand; %随机初始化位置 v(i,j)=(ub(j)-lb(j))rand*0.5; %随机初始化速度 end end end end

```

MOPSO

MOPSO及pso可编译运行matlab源码，及相关论文资源

1.0 版本 pso 部分

2.0版，MOPSO部分，文件在这 main.m

决定走前端这条路了，不过MOPSO我还是有研究了很久的，大概因为是本科实力不够吧，创新无力，所以只能做到复现，就到这吧，留下这篇文章，后来者少踩点坑吧。

看到MOPSO了，想必已经了解了PSO了，不需要要再赘述这些是什么了。

介绍下 下面的MOPSO文件吧

介绍下下面的MOPSO文件吧